CS 6104 : Solutions to Homework Assignment 1
June 5, 1998
CS 6104: Algorithmic Number Theory
Use the techniques in Chapter 2 to derive an asymptotic estimate for
where 
is an integer.
For 
and 
,
use Mathematicato compute h(x,k) precisely.
Present these results in a table
along with the values of your asymptotic estimates.
Recall Theorem 2.7.1, which states that for continuously differentiable functions g,
where 
.
Fix an integer , and set 
.
Then (1) becomes:
First, let us estimate the integral 
.
We will use Theorem 2.6.1 with 
. We have
We may take 
in the theorem. Since 
, we obtain
Knowing that , it's obvious that the
two error terms 
and
are each 
.
Hence, we have
The following Mathematica code computes h(x,k) precisely for the given values of x and k:
In[1]:= h[x_,k_] := Module[
{sum, i},
sum=0; i=2;
While[ i <= x,
If[ PrimeQ[i], sum = sum + i^k, ];
i = i + 1
];
sum]
In[11]:= Table[h[10,k],{k,1,4}]
In[12]:= Table[h[50,k],{k,1,4}]
In[13]:= Table[h[100,k],{k,1,4}]
In[14]:= Table[h[200,k],{k,1,4}]
The following code computes approximations for h(x,k) using the formula just derived:
n[18]:= ah[x_,k_]:=N[x^(k+1)/((k+1)*Log[x])]
In[19]:= Table[ah[10,k],{k,1,4}]
In[20]:= Table[ah[50,k],{k,1,4}]
In[21]:= Table[ah[100,k],{k,1,4}]
In[22]:= Table[ah[200,k],{k,1,4}]
The exact results produced by Mathematica are as follows.
The approximations produced by Mathematica are as follows.
Let R be the ring 
,
and consider the polynomial ring R[X].
Let 
be the polynomial
Finally, let
We claim that I=J.
To see this, take any 
. Letting g=p and h=1 in the
definition of I shows that 
. Similarly, for any
, note that g(x)f(x)h(x)=(g(x)h(x))f(x).
Taking p(x)=g(x)h(x) shows that 
.
The proof that I is an ideal is now identical to the proof given in class that J is an ideal. We repeat that proof here for completeness.
Certainly 
, so J is non-empty.
Suppose 
and 
are arbitrary elements in J.
Then
using the distributive law and the fact that
. So J is closed under addition.
Similarly, if 
and 
, then
using the associativity of multiplication and the fact that
. So J is closed under multiplication
by elements of R[x]. Hence, J=I is an ideal in R[x].
To see that these nine elements are distinct, observe that I consists
of all multiples of 
. Nonzero multiples of I will clearly
have degree at least 2, since the coefficient ring has no zero
divisors. Thus, the difference of two distinct elements of the
form 
is not in I, since this difference is a nonzero
polynomial of degree less than 2.
Next, T does not have any additional elements. For, any polynomial
of degree 2 or more is equivalent to one of the polynomials listed
above, since we can reduce modulo f to replace 
by -2=1,
by x, etc.
, etc.)
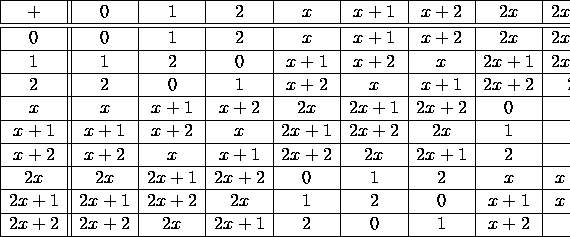
This first table is easily computed by noting that 3=0 in the coefficient ring.
The multiplication table for T is easily computed if we remember
to replace by 1 whenever it appears in a product. We get:
Chapter 3, Problem 8.
where f(x) is this polynomial
The problem specification did not require a proof on why this works,
so I haven't provided one! In a nutshell, however, this algorithm
works because when x ;SPMgt; 0, 
. This means that when
x ;SPMgt; 0, the function is increasing, and hence we can rely on the
fact that, if f(a) ;SPMlt; n, then f(x) ;SPMlt; n for all 
.
Similarly, if f(a) ;SPMgt; n, then f(x) ;SPMgt; n for all 
. This
allows us to use a binary search to find the solution.
This algorithm, in the worst case, is clearly 
, since
all it does is start with a search range of [0,n], and then it
uses a binary search to repeatedly half the range until it either
finds an x such that f(x) = n or it reduces the search range to
a single integer. Everything outside of the while loop in the program
will run in constant time.
The represents the worst case number
of calls to the function f, which I am assuming also runs in a constant
amount of time.
(************************************************************************
Function DiophantineSolve takes as parameters a function f and an
integer n, and returns either a non-negative integer x such that
f(x) = n or -1 if no such non-negative integer exists.
************************************************************************)
DiophantineSolve[f_, n_] := Module[{},
(* Set the range of integers in which we will find our answer *)
rbegin = 0;
rend = n;
(* Choose our initial guess *)
index = Floor[(rend+rbegin)/2];
val = f[index];
(* Search until we find an answer or run out of integers *)
While[(rbegin != rend)&&(val != n),
(* If the search range was of length 1, make it length 0 *)
If[(rend-rbegin) == 1, rbegin = rend,
If[ val > n, rend = index - 1, rbegin = index + 1]
];
index = Floor[(rend+rbegin)/2];
val = f[index];
];
(* Set -1 as the return value if no answer was found *)
If[ val != n, index = -1];
index
]
(* Here we define f *) f[x_] := 14x^17 + 99x^7 + 3x^2 + 94 (* Now we can solve part C on the homework *) DiophantineSolve[f, 33110401974639861466556783753600023154051803888587048939300]The Mathematica function found the solution:
