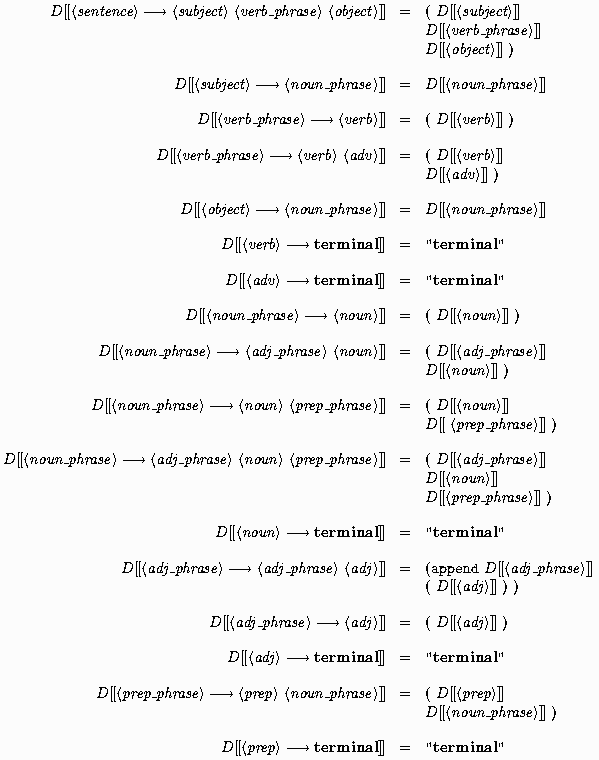
| Home | Notes | Languages | Programs | Homework |
| Program Assignment 2 |
| Problem |
Once again, you will be diagramming sentences that match the grammar described for Program 1.
| Implementation Language |
For this assignment, the implementation language is Scheme. You will be programming in a "functional" style, as described in Chapter 14 of the text book. Since this program must be written in Scheme, appropriate use of functional language features is expected. Hence,
set!, setcar!, setcdr!, and all
other operations with named ending in "!" are not allowed.
do and
begin. That still leaves you with plenty of control
structures to work with, though.
Here are some suggestions:
cond or if. The
if function is a special case of cond. If
you only use cond, you'll probably never miss
begin.
let. That
means using recursion in spirit whenever you need to repeat
a series of actions. Alternatively, you can define a separate
recursive function if you prefer.
let (instead of begin). This most
commonly arises if you
use an if instead of cond, which is one reason that
cond is often preferred.
| Input Format |
Write your program as a Scheme function called
diagram-sentence. Your function should take a single
argument, which is a list of strings that represents the input to be
diagrammed. For example, you might invoke your sentence diagrammer
with the following S-expression:
(diagram-sentence '("Alice" "found" "mean" "green" "book"))
This setup differs slightly from Program 1, in that you are no longer responsible for reading from standard input or splitting a line into individual tokens (words).
p2-in.scm is a sample segment of Scheme
code that illustrates how your diagram-sentence function
will be invoked by the Curator during electronic grading.
One way to organize your solution (but not the only way, and certainly not a requirement for this program) is to construct one procedure for each nonterminal that takes a list of strings as a parameter and breaks the list into a diagram for that nonterminal (if possible) and the remainder of the string. For example:
(define (adj list-of-strings)
(cond
((null? list-of-strings) ())
((string=? (car list-of-strings) "green")
(list "green" (cdr list-of-strings)))
((string=? (car list-of-strings) "lean")
(list "lean" (cdr list-of-strings)))
((string=? (car list-of-strings) "mean")
(list "mean" (cdr list-of-strings)))
(else ())
)
)
The procedure adj
does the job for <adj>.
A sample invocation of adj is
(adj '("green" "cow" "saw" "book"))
which returns
("green" ("cow" "saw" "book"))
Scheme procedures that you may want to use include
apply car cdr cond cons
define equal? list map not
null? number? + < string=?
| Output Format |
For purposes of our Scheme implementation, the "diagram" produced by your program will be an S-expression that represents the grammatical structure of the sentence. For example, consider the following sentence:
mean cow saw carefully green Alice with book
the S-expression for this sample should be
((("mean") "cow") ("saw" "carefully") (("green") "Alice" ("with" ("book"))))
Your diagram-sentence function should return such an
S-expression, or list structure, as its value for a sentence that
parses successfully, or return a string containing the appropriate
error message if the input is in error.
p2-out.txt shows the expected output produced
by evaluating the p2-in.scm input in the context of a
correct diagram-sentence definition.
We can define a denotational semantic function D that gives the meaning of a parse tree for the Program 1 grammar as a diagram represented by a Scheme S-expression. In particular, the denotational semantics function D takes a subtree of the parse tree as argument and returns an S-expression.
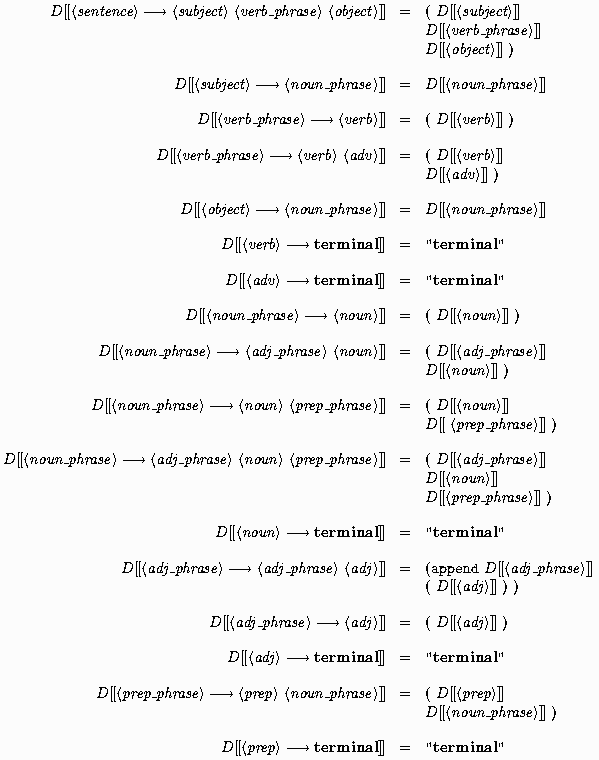
Some explanation of the denotational semantics is in order. While the argument to D is always a subtree of a parse tree, the definitions only give the meaning of the subtree in terms of the children of the root. In particular, the argument of D on the left of a definition is the production used at the root of the subtree and the arguments to D on the right of a definition give the nonterminals that represent the roots of the subtrees. For example, the definition
![]()
covers the case of a parse tree
having <sentence> as the root,
which has children <subject>, <verb_phrase>,
and <object>$.
The production used is of course
<sentence> --> <subject> <verb_phrase> <object>
which is mentioned explicitly in the argument to D for clarity. The meaning attached to the parse tree is
![]()
which is an S-expression (notice the parentheses) of length 3
having elements that are the meanings of the three subtrees
with roots <subject>, <verb_phrase>,
and <object>.
Note the use of the Scheme append function in one of the semantic
definitions to indicate concatenation.
Finally,
the terminal terminal is just meant to match
any of the appropriate terminals (words) from the grammar.
Now we can apply the denotational semantics above to an example to show how the resulting S-Expression is derived. Consider parsing this sentence:
Alice found mean green book
The resulting output should be:
(("Alice") ("found") (("mean" "green") "book"))
The denotational semantics for this sentence are derived below:

| Submitting Your Program |
Your program will be submitted electronically through the Curator for automatic grading against a randomly generated test suite. To submit your program, login to the Curator using your PID and password. Be sure to select the 11374-CS 3304 11:15 MWF Edwards section when logging in. Click on "Submit", choose Scheme2 from the project drop-down list, click "Browse" to specify your solution, and then click "Upload."
In addition, you must also turn in a printed version of your
program source in class according to the rules specified in the
syllabus, which also describes the late policy.
| Home | Notes | Languages | Programs | Homework |