CS 6104 : Solutions to Homework Assignment 3

June 9, 1998

Problem 1. [Solution Courtesy of Duxing Cai]

Chapter 5, Problem 24. Do not look up the answer. Think about the Chinese Remainder Theorem.

Also, derive all solutions for n=30.

Solution:

Let , where are powers of distinct primes. We know:

Note that, are relatively prime, we have:

i.e. The solutions of are equivalent to the solutions of the systems:

So the numbers of solutions should be the same. Also note that:

So the solution of must satisfy: or
.

i.e. For each we have two choices. So we can get different systems:

where or 1.

By the Chinese Remainder Theorem, each system must have one unique solution modulo . Furthermore, by the Extended Chinese Remainder Theorem we know these systems have distinct solutions. Actually, if two different system have the same solution x, then within these two system must exist the following two different equations associated with some :

But this is impossible.

So we can conclude that the equation (mod n) has exactly different solutions. Now we can derive all solutions for n=30:

Since n=30=2*3*5, we can get the following systems:

• 
• 
• 
• 
• 
• 
• 
• 

With the Extended Chinese Remainder Theorem, system (1) can be reduced to the following system:

Since , we get: t=3*h for some h. So the system becomes: . Thus the solution of this system is:

Similarly we can find all the other solutions as following:

Problem 2. [Solution Courtesy of Cara Struble]

Use Theorem 5.8.1 to compute the Legendre symbol

is two distinct ways. If

then find a solution x to the congruence

(Consult Theorem 7.1.1 and Corollary 7.1.2.)

Using Theorem 5.8.1, there are many different ways to compute a Legendre symbol. The first method I present is simple and direct. Using rule (1), we have

Mathematicacomputes the right hand side of the equivalence to be 1, so the Legendre symbol is 1.

Another way to compute the Legendre symbol is to break up 958816 using rule (2). The number 958816 has prime factorization . So

Now we can look at each of these individually. Using rule (5),

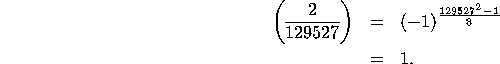
So

Since 129527 does not divide 19, we can apply rule (4) and get

Since 83 is prime, rule (6) can be used to flip the numbers and the sign is determined by raising -1 to . This power comes out odd so we have

Next we apply rule (3), choosing b = 47 so that . And we get

Using rule (6), we once again get -1 to an odd power, so

Now rule (3) applies again if we choose b = 36 because . So

Since 36 is and 47 does not divide 6, we can apply rule (4) and get that

Thus,

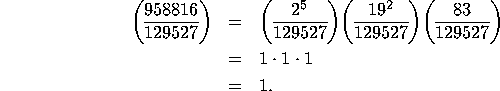
The second part of the problem is to solve

which can be simplified to

Now Corollary 7.1.2 can be applied to solve for x: