This page is an addendum to the class discussion of September 28, 2001, when the Aho-Corasick algorithm was described and an example worked out.

• Our example is the set

  P = {potato, tattoo, theater, other}

  also used in the textbook. We built the keyword tree K
  

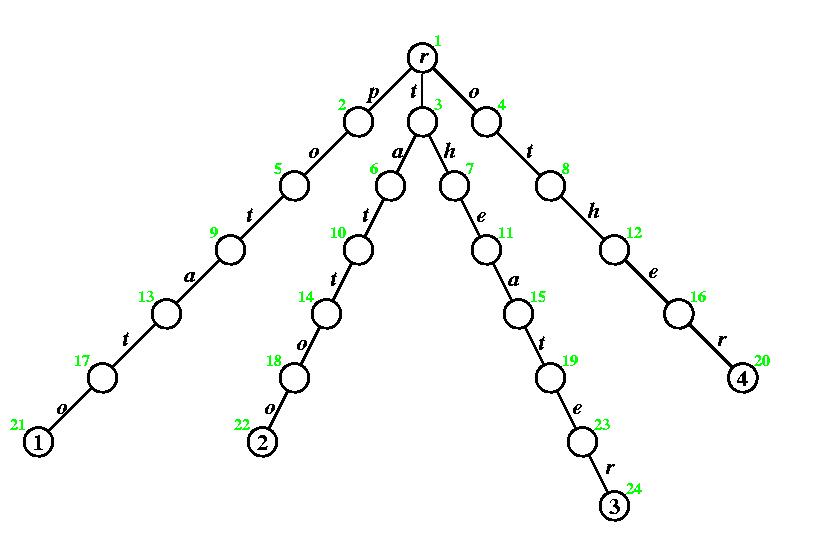
  which is also found in Figure 3.16. We determined the failure links, which are found in Figure 3.16 as well (links that go to the root are omitted for clarity).

  We added the breadth-first labels 1, 2, ..., 24 to uniquely identify all 24 nodes.

• Here is the pseudocode given in class that corrects the algorithm on page 56 of the text.

  l = 1        # Index in T of the first character in the current path
  c = 1        # Index in T of the next character to compare
  w = 1        # Node in K at which the current path ends
  
  repeat
  
      while there is an edge (w,w') labeled T(c) do
          if w' is labeled by pattern i then
              print "Pattern i occurs at position l."
          w = w'   # Descend further down into the tree
          c = c+1  # Ready for the next character in T
  
      if w=r then  # T(c) could not be matched,
          c = c+1  # so go to the next character in T
  
      w = nw       # Follow the failure link
      l = c - lp(w)    # Adjust the value of l
  
  until c>m
  

  The essential addition is the conditional

      if w=r then  # T(c) could not be matched,
          c = c+1  # so go to the next character in T
  

  which takes care of the special case when the path has length 0.

• A good way to identify the workings of the algorithm is to document each change in w, the current node in K. In particular, w descends deeper into the tree whenever a character in the text is matched, while w takes its next value from its failure link whenever a character in the text fails to match. The following table documents these changes in w when the text is the string othxxpotattootheryy.

  w	1	4	8	12	7	1	1	1	2	5	9	13	17	10	14	18	22	4	8	12	16	20	1	1	1
  c	1	2	3	4	4	4	5	6	7	8	9	10	11	11	12	13	14	14	15	16	17	18	18	19	20
  T(c)	o	t	h	x	x	x	x	p	o	t	a	t	t	t	o	o	t	t	h	e	r	y	y	y	-
  l	1	1	1	1	2	4	5	6	6	6	6	6	6	8	8	8	8	13	13	13	13	13	18	19	20

  The matches reported by the algorithm are

  Pattern tattoo occurs at position 8.
  Pattern other occurs at position 13.

Please report any problems found in these pages to: