CS 5114 Homework 5 (Spring 2009)

Describe your algorithms as clearly as possible. The style used in the book is fine, as long as your description is not ambiguous. Do not make any assumptions not stated in the problem. If you do make any assumptions, state them clearly, and explain why the assumption does not decrease the generality of your solution. If you use any new words or phrases, define them, especially if we have not used these words/phrases in class. Do not describe your algorithms only for a specific example you may have worked out. You must also provide a clear proof that your solution is correct (or a counter-example, where applicable). Describe an analysis of your algorithm and state its running time. You will only get partial credit if your analysis is not tight, i.e., if the bound you prove for your algorithm is not the best upper bound possible.

1. (20 points) Solve exercise 1 in Chapter 6 (pages 312-313) of your textbook.
2. (30 points) Solve exercise 17 in Chapter 6 (pages 327-328) of your textbook.
3. (50 points) A convex polygon is a polygon where very interior angle is less than 180 degrees. A museum is in the shape of a convex polygon with n vertices. The museum is patrolled by guards. The Directory of Security at the museum has the following rules to ensure the most safety in as time-economical a way as possible:
   1. Each guard traverses a path in the shape of a triangle; each vertex of such a triangle must a vertex of the polygon.
   2. A guard can survey all the points inside his or her triangle and only these points; we say that these points are covered by the guard.
   3. Every point inside the museum must be covered by some guard.
   4. The triangles traversed by any pair of guards do not overlap in their interiors, although they may share a common edge.
   Given these constraints, the cost incurred by a guard is the length of the perimeter of the triangle the guard traverses. Our goal is to find a set of guards such that the total cost of the guards (i.e., the sum of the costs of the individual gaurds) is as small as possible. Given the x- and y-coordinates of the vertices of the art gallery and the ordering of these vertices along the boundary of the art gallery, devise an algorithm whose running time is polynomial in n to solve this problem. Note that we are not trying to minimise the number of guards; we want to minimise the total lengths of the routes patrolled by the guards. You may assume that the length of any line segment is the Euclidean distance between the end-points of the line segment and that this length can be computed in constant time.

   

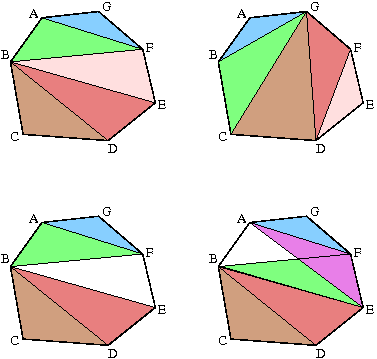
   Above are four figures that illustrate the problem. The museum is the polygon ABCDEFG. Each coloured (shaded) triangle corresponds to a guard and the guard will traverse the perimeter of his or her triangle.

   • The top two figures show a set of guards (their triangles) that satisfy the constraints laid down by the Directory of Security. In the top left figure, the guards traverse the boundaries of triangles AFG (blue), ABF (green), BEF (pale red), BDE (light red), and BCD (brown). In the top right figure, the guards traverse ABG (blue), BCG (green), CDG (brown), DFG (light red), and DEF (pale red).
   • The bottom two figures show a set of triangles that do not satisfy these constraints: in the figure on the bottom left, part of the museum is not covered by any guard (the unshaded triangle BEF) while in the figure on the bottom right, the pink triangle (AEF) and the green triangle (BEF) intersect (not that the part of the green triangle in the image is covered by the pink triangle).