CS 5114 Homework 5 (Spring 2008)

Describe your algorithms as clearly as possible. The style used in the book is fine, as long as your description is not ambiguous. Do not make any assumptions not stated in the problem. If you do make any assumptions, state them clearly, and explain why the assumption does not decrease the generality of your solution. If you use any new words or phrases, define them, especially if we have not used these words/phrases in class. Do not describe your algorithms only for a specific example you may have worked out. You must also provide a clear proof that your solution is correct (or a counter-example, where applicable). Describe an analysis of your algorithm and state its running time.

1. (40 points) The Headstrong Headless Horseman Problem (not to be confused with Ichabod Crane's problem with the Headless Horseman) is the following: The Horseman has to find his head, which he has hidden at one of n places in a forest. However, the Horseman has forgotten where he hid his head. He decides to search for it by travelling to each hiding place. Since the Horseman is familiar with Cartesian geometry, he knows the x- and y-coordinates of each possible hiding place. Being headstrong, the Horseman wants to
   1. start at the leftmost hiding place,
   2. return to this hiding place at the end of his search,
   3. visit each other hiding place exactly once, and
   4. start riding from left to right till he reaches the rightmost point and then ride from right to left till he reaches the leftmost point.
   Thus, his journey can be divided into two parts: in the first part, the x-coordinates of the places he visits keep increasing and in the second part the x-coordinates of the places keep decreasing. Note that the y-coordinate of a place he visits may be larger or smaller than the y-coordinate of the place he visits next. Assume that no two hiding places have the same x- or y-coordinates and that the horseman rides in a straight line from one place to the next.

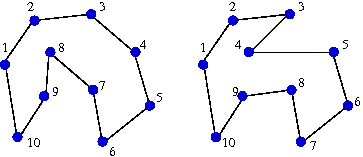
   The figure below shows two journeys, with the numbers indicating the order in which the horseman visits the hiding places. The tour on the left is legal. The tour on the right is not legal because the third point has an x-coordinate larger than that of the fourth point.

   

   You have recently moved to the forest. The Horseman asks you for help. Devise an algorithm that will compute a journey of shortest length that satisfies the Horseman's constraints (otherwise, you will lose your head).

2. (30 points) Solve exercise 6 in Chapter 7 (pages 416-417) of your textbook.
3. (30 points) A flow network has m edges. Show that there exists a sequence of at most m augmenting paths that yield the maximum flow. In other words, if you prove this statement, you would have shown that if the augmenting paths were chosen correctly (by magic), the Ford-Fulkerson algorithm will terminate in at most m iterations. Note that this question is not algorithmic: you do not have to demonstrate an algorithm to compute these augmenting paths.