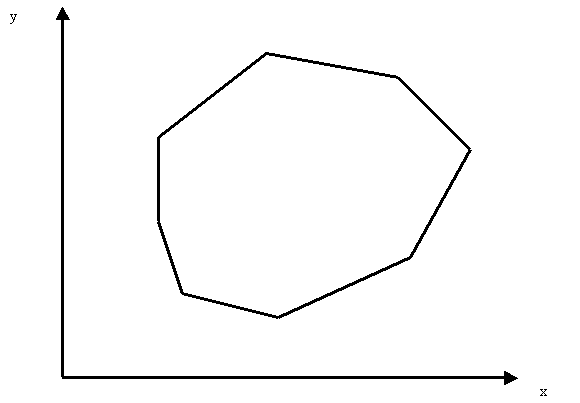
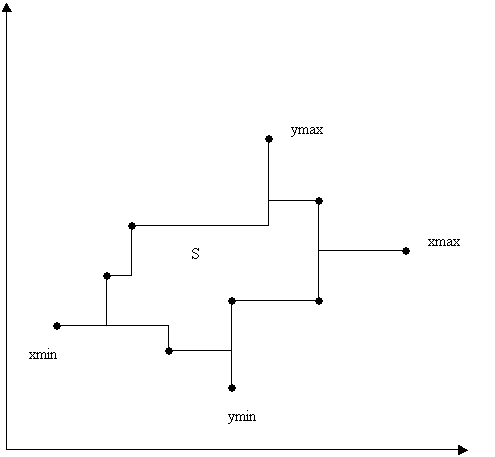
CONVEX HULL ALGORITHMS

Definition: The convex hull of a planar set is the minimum area convex polygon containing the planar set.

Consider set of points S = { x_i y_i}

i = 1, 2, …, n

NOTE: For a point (x, y) to be a VERTEX (i.e on the convex hull) the exterior angle formed by joining (x, y) to its immediate neighboring vertices must be > 180^o (p)

3 CONVEX HULL ALGORTIHMS

I. R. L. Graham (1972)

Information Processing Letters V1, p132-133

II. R. A. Jarvis (1973)

……………………………..……V2, p18-21

III. S. G. Akl and G. T. Toussant (1978)

……………….………………….V7, p219-222

I. Graham’s Algorithm

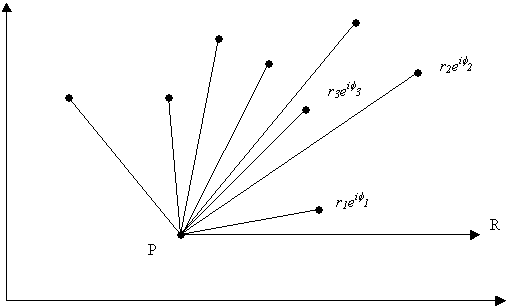
Step 1: Find the bottommost point P

T = c₁n

Step 2: Express each (x_i, y_i) Î S in polar

coordinates with origin P and f = 0 in the direction of R T = c₂n

Step 3: Order the elements r_ke^ifk of S in terms

of increasing f_k to give:

S = { r₁e^if1, r₂e^if2, …, r_ne^ifn}

T = c₃n log n

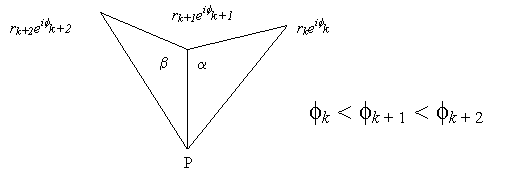
Step 4: Consider 3 consecutive points in S

2 possibilities:

(i) a + b ³ p Delete point (k + 1) from S and

return to step 4 with points

(k - 1), k , (k + 2)

(ii) a + b < p Return to step 4 with points

(k + 1), (k + 2), (k + 3)

Step 4 either reduces number of possible points of CH(S) by one

or increases the total of S points

considered by one

T(n) < 2 n

Total T(n) = k₁n + c₃n log n

II Jarvis Algorithm

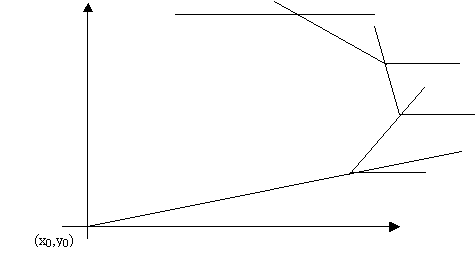
Step 1: Find an origin point outside the set S

e.g. x₀ £ min { x_i } y₀ £ min { y_i }

T = c₁n

Step 2: Find (x_k, y_k) such that

q_0k £ min { q_0i } i = 1, 2, …, n

where q_0i is the angle measured with

respect to a horizontal axis through

(x₀, y₀)

Step 3: Shift origin to (x_k, y_k) and repeat step 2

with consistent angle direction and

origin until 1^st convex hull point is

re-found

T = (m + 1)n for m convex hull points

Improvements

(1) Point Deletion

After step 2 has been completed once and 1^st CH point identified, evaluate and store the angles of lines from the 1^st CH point to the (n – 1) other points. Then within step 2 after the 1^st iteration, any point whose angle calculated and stored is < the last found CH point cannot be a valid candidate for a CH point.

Example n = 29 m = 9

n(m + 1) = 290

(2) Obviating actual angle evaluation

	opposite side adjacent side

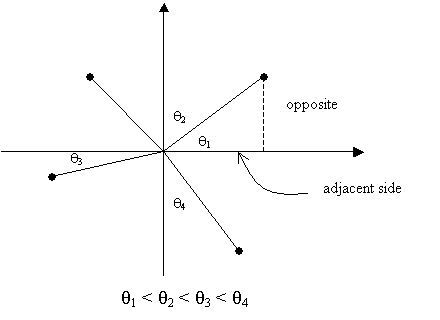
[Keep a list of for the right-angled D’s]

(i) check the signs of (x_i – x₀) and (y_i – y₀)

(i=1,2,…, n) to determine the quadrant

opp. side for quadrants

adj. side 1 & 3

inverse 2 & 4)

(ii) keep only the lowest ratio (

for the lowest quadrant yet detected when

working through the points.

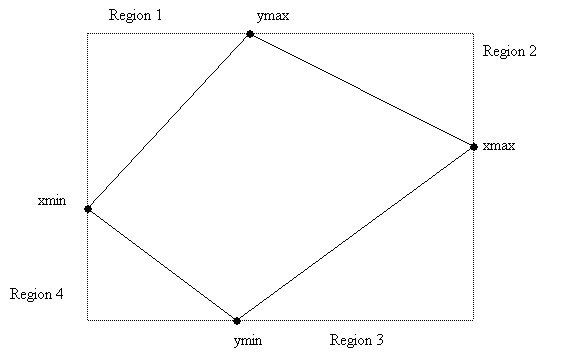
III AKL and TOUSSANT algorithm

Vector cross product

C = a b sin q = a b sin (a₁ + a₂)

= (y_k+1 – y_k) (x_k+2 – x_k+1) + (x_k – x_k+1) (y_k+2 – y_k+1)

C

L. H. diagram R.H. diagram

+ ve - ve

If C ³ 0 keep point (k + 1) else delete it

Step 1: Find the extremal points and delete all

other points falling inside the polygon

they form. T = c₁n

Step 2: Sort the remaining points on their x

co-ordinate: in ascending order for

regions 1 & 2 and decreasing order for

regions 3 & 4. T = å c_i n_i log n_i

Step 3: For each region find the convex path

from one extremal point to the next

Generally for every 3 consecutive points

k, k + 1, k + 2

(i) Compute C

(ii) If C ³ 0 move 1 point forward

else delete point (k + 1) and move

1 point backward.

T = å c_i n_i

Advantages

(i) For large n approximately ½ the points are

discarded in Step 1

(ii) Breaking the problem into sub-problems by

distributing the points into the different

regions makes it easier and faster to solve

(good example of DIVIDE & CONQUER)

(iii) The cross product criterion is simple and

inexpensive compared to computation of

angles, shifting the axes.

Timings for 100 runs in seconds

Uniform Within Square N	250	500	1000	2000
I	1.18	2.39	4.78	9.78
II	2.62	6.02	13.21	29.02
III	0.91	1.73	3.37	6.54

Uniform Within Annulus N	250	500	1000	2000
I	1.17	2.24	4.69	9.44
II	6.65	16.37	52.63	104.86
III	2.05	4.35	9.50	20.74

Convex N-gon N	250	500	1000	2000
I	1.01	2.01	4.02	8.16
II	42.5	164	674	2615
III	2.3	4.82	10.28	21.60

Problems in computational geometry related to the convex hull

Given a set of N points in the plane determine:

(i) the rectangle of minimum area which will completely cover (or encase) the set (MER)

(ii) the diameter of the set (the 2 points which are furthest apart)

(iii) the shortest tour which will visit each point once and return to the starting point (the classical Traveling Salesman Problem)

Problems (i) and (ii) may be solved by a common technique: the HIGHPOINT STRATEGY

This leads to efficient algorithms for both problems because all highpoints can be found in O(n) time.

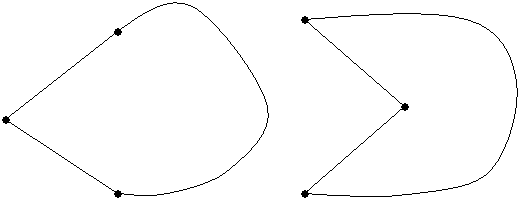
Highpoint Strategy

Given a convex polygon, determine the vertex point(s) which has (have) the greatest perpendicular distance above each edge.

Algorithm for highest points

1. Locate the highest point(s) above an initial edge i j of the polygon

2. (Highpoint strategy) move to the next edge, let i = j, j = cclock(i), and find its highest point(s). Start the scan at the highpoint from the previous edge (or left highpoint if there are 2). Repeat step 2 until initial edge is reached.

Question: Find the MINIMUM

ENCASING RECTANGLE for a

set of N points in the plane

The Minimum Encasing Rectangle

Theorem: (Freeman and Shapira) The minimum area encasing rectangle of a convex polygon must have one side collinear with an edge of the polygon.

Algorithm:

Step 1: Compute the convex hull of the set

Step 2: Compute the encasing rectangle

collinear to each edge and take

smallest as MER

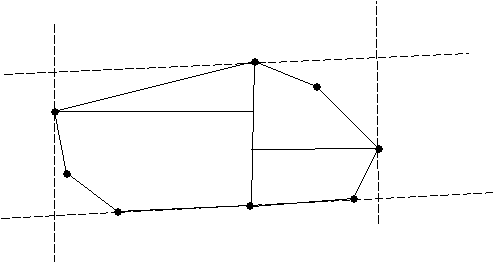
Area of encasing rectangle collinear to edge i j is

l * (w₁ + w₂)

Strategy:

1. Move to next edge. Let i = j, j = cclock(j)

To find new highpoints A, D, and B; use the

previously determined highpoints as the

starting points for the new highpoint scans.

Compute the NEWAREA.

2. Apply process to each edge.

Average time to find MER for uniform random points on the boundary of ellipse

N	Time (for 100 runs in secs)
125	3.556	(.0114)
250	7.096	(.0344)
500	14.184	(.0532)
1000	28.116	(.0729)

(ii) The Diameter of a Set

N = N(N-1) ~ O(N²)

2 2

One possibility: Examine the distance between all possible pairs of points

Theorem: (Hocking) The diameter of a set

must be realized by 2 points on its convex

hull.

Theorem: (Yaglon) The diameter of a

convex polygon is the greatest distance

between parallel lines of support.

Definition: A line L is a line of support of a

polygon P if it meets the boundary of P and

P lies entirely on one side of L.

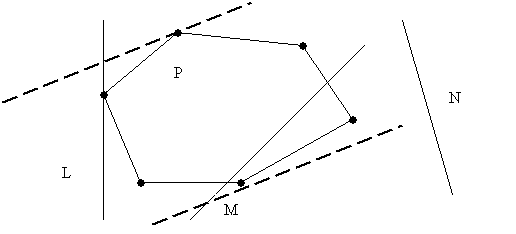
L supports P, M and N do not.

Two lines of support parallel to a given direction

Algorithm DIAM

1: Find the convex hull of the set

T(n) ~ O(n log n)

2: Enumerate all pairs of vertices for which

parallel lines of support exist (referred to by

M. I. SHAMOS as antipodal pairs) and take

the pair separated by the largest distance.

Assuming N points are on the hull, step 2 may be computed in O(N) time by applying the HIGHPOINT strategy and the following observation:

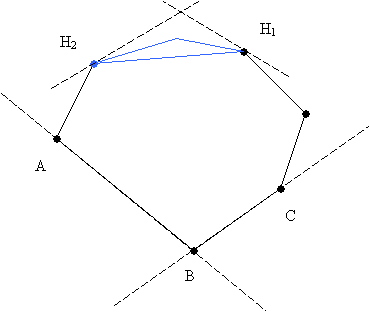
In the figure AB and BC are the lines of support of vertex B. Let the highest points above these two lines be H₁ and H₂ respectively. Because of the convexity property of the hull, parallel lines of support to AB and BC can pass through H₁ and H₂. Thus (B, H₁) and (B, H₂) are antipodal pairs. Only the chain of points on the convex hull between H₁ and H₂ will admit to parallel lines of support in conjunction with point B (blue triangle).

Algorithm DIAM

1: Start with the bottom most point i on the hull and its two common edges. Find the highest point above each edge. Label these points H₁ and H₂. Compute the interpoint distances between i and all vertices in the chain H₁ … H₂. Keep only the largest of these distances L and its corresponding antipodal pair (i, H_i) where H_i is the farthest point from i.

2: Let i = cclock(i). Find the highest point above each edge adjoining i. Set H₁ = H₂ (or H₁= clock(H₂) if two highpoints) and use the HIGHPOINT strategy to find H₂. Compute distances between i and all vertices in the chain H₁…H₂. As the values are computed, compare with the largest pair already in storage, and if necessary, reassign L and the corresponding pair. Repeat step 2 until i = H_i

Why stop at H_i?

Performance of DIAM

For uniform random points generated on the boundary of an ellipse

For each sample size all points remained on the hull. 5 tests of 100 runs were carried out for each sample size

N	DIAM	SHAMOS Algorithm
125	.466 (.0089)	.698 (.0048)
250	.926 (.0152)	1.432 (.0164)
500	1.832 (.0130)	2.886 (.0207)
1000	3.644 (.0462)	5.810 (.0678)
2000	6.990 (.0914)	11.762 (.1180)

times in seconds for 100 runs

(iii) The Euclidean Traveling Salesman

Problem

Known results (enumeration is O(N^N)!)

1. The shortest tour cannot intersect itself

2. The order in which the points of S forming

the vertices of the convex hull appear in the

shortest tour is the same as the order in

which they appear along the boundary of the

convex hull.

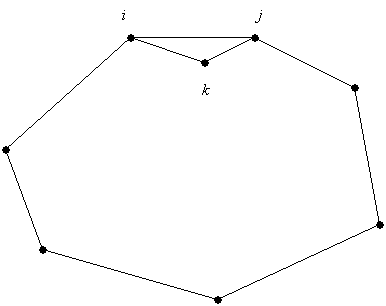
Procedure HULL_HEURISTIC (S, n, T_m)

BEGIN

Step 1: Form the convex hull of S. Let m =

number of points on the hull and let the

hull be initial subtour T_n.

Step 2: WHILE m < n DO

BEGIN {insertion phase}

Step 3: For each point k not yet

contained in T_m find two

consecutive points i, j Î T_m on the

subtour such that d₂(i, k) + d₂(k, j) –

d₂(i, j) is minimal.

Step 4: From all the (i, j, k) found in

step 3 determine the (i^*, j^*, k^*) such

that [d₂(i^*,k^*) + d₂(k^*,j^*)]/ d₂(i^*,j^*) is

minimal

Step 5: Let T_m+1 = T_m + k^* {insertion

of k^* into T_m between node i^* and j^*}

Step 6: m = m + 1

END {WHILE loop}

END {Hull_Heuristic – T_m contains ETSP tour}

Depending on inputs, procedure takes from O(n²) to O(n³) to compute T_n.

The L₁ Traveling Salesman Problem

(sometimes called the Manhattan metric)

The distance between any 2 points (x_i, y_i), (x_j, y_j) is d₁(i,j) = | x_i – x_j | + | y_i – y_j |

To find a tour of minimum distance, first compute the L₁ hull, and use it as the initial subtour. Then call a modified PROCEDURE HULL_HEURISTIC (with distance function d₁ rather than d₂)

Performance

L₁ TSP tested against two heuristics which have been used to solve the ETSP (L₂ TSP) – nearest insertion and farthest insertion.

Random number generator used to generate points uniformly throughout the unit square for different N.

Quality of each algorithm measured by:

Efficiency = (length of tour)/ B where B=1.102*length of minimum spanning tree

N	Nearest Insertion	Farthest Insertion	Hull Heuristic
25	1.248	1.238	1.168
50	1.184	1.200	1.132
100	1.186	1.192	1.114
200	1.178	1.181	1.119
400	1.177	1.181	1.128

PROBLEM 1

Given a rectangle containing n points, find the largest subrectangle with sides parallel to those of the original rectangle which contains none of the given points.

Rectangle A

Points (x_i, y_i) i = 1,n

Definition: A rectangle M is a RESTRICTED RECTANGLE (RR) if:

1. M is completely contained in A

2. M contains no points (x_i, y_i) in its interior

3. Each edge of M either contains a point (x_i, y_i) or co-incides with an edge of A.

Lemma: The number of RR’s is bounded by O(n²) where n is the number of points.

There are 4 types of RR’s.

1. RR’s in which 2 opposite edges co-incide

with edges of A

(at most 2n + 2)

2. RR’s in which 2 adjacent edges co-incide

with edges of A

(at most 2n + 2)

3. RR’s in which exactly 1 edge co-incides with

an edge of A

(at most 4n)

4. RR’s in which each edge contains a point

(x_i,y_i) in its interior.

(at most O(n²))

If the points are drawn randomly and independently from a rectangle A, the expected number of RR’s is O(n log n)

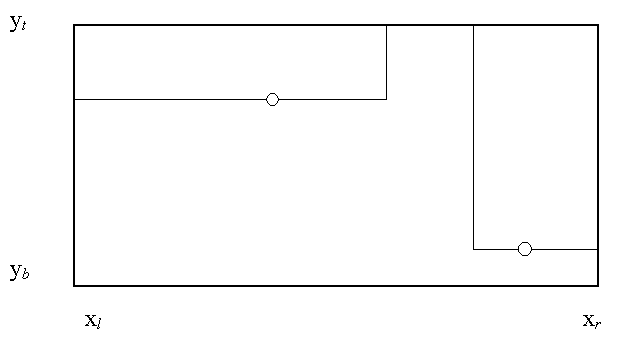
An O(n²) sweep-line algorithm (Naamad, Hsu, Lee)

1. Find maximum gap in x co-ords, MGAP

MAXR = MGAP * (Y_t – Y_b)

2. Sort points on y co-ords in descending order

3. for i = 1 to n do

T_l = x_l, T_r = x_r

for j = i + 1 to n do

if T_l < x_j < T_r then

MAXR = max (MAXR, (T_r – T_l)*(Y_i – Y_j))

if x_j > x_i then T_r = x_j else T_l = x_j

MAXR = max (MAXR, (T_r – T_l)*(Y_i – Y_b))

4. for i = 1 to n do

R_i = min (x_r U x_j where x_j > x_i y_j > y_i) {look }

L_i = max (x_l U x_j where x_j < x_i y_j > y_i) {look }

MAXR = max (MAXR, (R_i – L_i)*(Y_t – Y_i))

{rectangles with top as one side}

An O(n log³ n) algorithm

(Chazelle, Drysdale, Lee)

· used divide-and-conquer

· split points into 2 halves by x co-ordinate and solve recursively

· problem is rectangles crossing dividing line

These rectangles have either

3 supports in one half, 1 in other

or 2 supports in each half

Let C(n) = time to find largest rectangle with 3

supports in one half, 1 in other

D(n) = time to find largest rectangle with 2

supports in each half.

T(n) £ 2T(n/2) + C(n) + D(n)

O(n) O(n log² n)

T(n) = O(n log³ n).

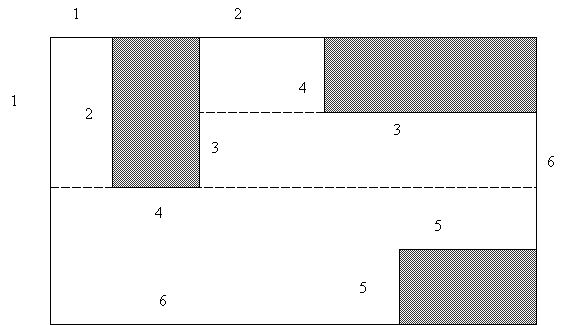
PROBLEM 2

Given a set of rectangles within a similar rectangle, find the maximum empty rectangle which remains.

SWEEP LINE ALGORITHM

1. Set-up Edges

Horizontal Edges

(x1, x2, y, facing, x1open, x2open)

Vertical Edges

(y1, y2, x)

2. Pre-Processing

a. Sort horizontal edges

b. Sort vertical edges

c. Replace downward facing horizontal edges by sweeplines

3. Sweep

Scan horizontal edges from top and build list of downward facing edges

if edge is downward then

add to list

else {at least one rectangle must be formed}

scan list

if overlap then

compute area of rectangle

shorten or delete downward edge

List Rectangles

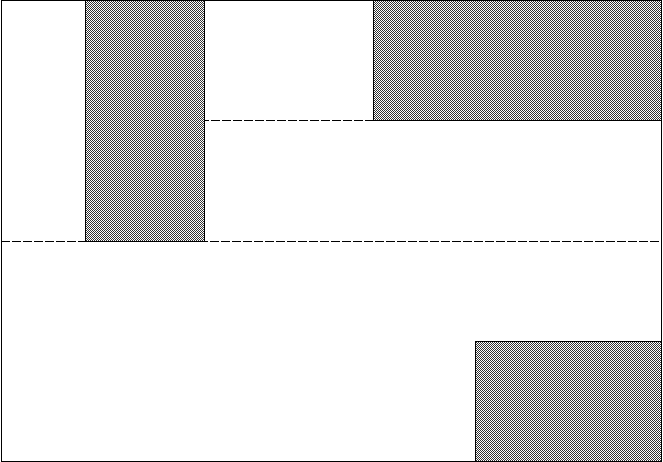
Worst Case n = # horizontal edges

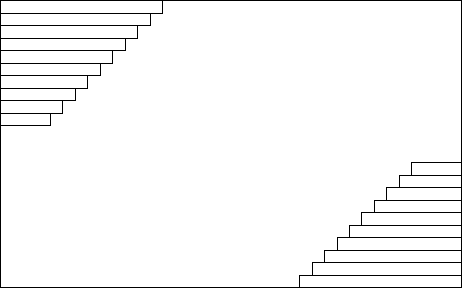
# Rectangles = ¼ n²

Best Case

# Rectangles = n + 1

Strategy for Placement

(i) in adjacent corners

(ii) side by side