Submission Date: Friday, April 22, 2016, 23:55
See the Requirement Guidelines for In-Class Exercise (ICE) assignments.
This is an in-class group assignment. Fill in the names and email PIDs of the group members in the space provided below so that each group member knows who is in the group. Submit one copy of this to your instructor before you leave class.
| Group member name | Role | VT Email PID |
| Solver | ||
| Recorder | ||
| Coordinator/Listener | ||
| Presenter/Listener |
Pick a solver and a scribe for your group; the remaining members will play the role of listeners. Identify the role taken by each group member in the table above.
Follow the Solver/Listener paradigm to analyze and attempt to solve the given problem. It is important that you manage the discussions in a disciplined manner so that the scribe can take adequate notes to prepare a transcript of your session.
When you believe you have a solution to the problem, work together to prepare an outline to help the solver present your results to the class.
After the class, and by the announced deadline, prepare a written presentation of your session, including the interactions between the solver and the listeners and a detailed explanation of how you arrived at your solution. You may include diagrams and mathematical work if you used those as part of your process.
Only one group member, the scribe/recorder, must submit that to moodle via the collection point for Hw12-ICE03. The scribe must ensure that their group partners names and email PIDs are at the top of the first page of the submission.
Remember that the evaluation of your solution will depend primarily on the completeness and clarity of your explanation.
For this assignment groups will work to solve one of three different types of game.s
The Games
A. Sokoban
Sokoban is a warehouse packing game. The goal of the game is to push boxes/crates to designated locations. It requires logical deductive reasoning to solve. There are many variations and implementations of sokoban.
For the purposes of this assignment we will use the freeware implementation for MS Windows Ben Ruyl Sokoban 3.0. It is available for download at ben-ruyl-sokoban.en.softonic.com. (Be forewarned that during installation it will install a toolbar if you do not uncheck the option for doing so.) It comes with several skins. The default skin is Jumanji. The screenshots below use the AntiqueDesk3 skin. (Do NOT use the MS DOS skins as they are difficult to view.)
The starting screen for level one is:
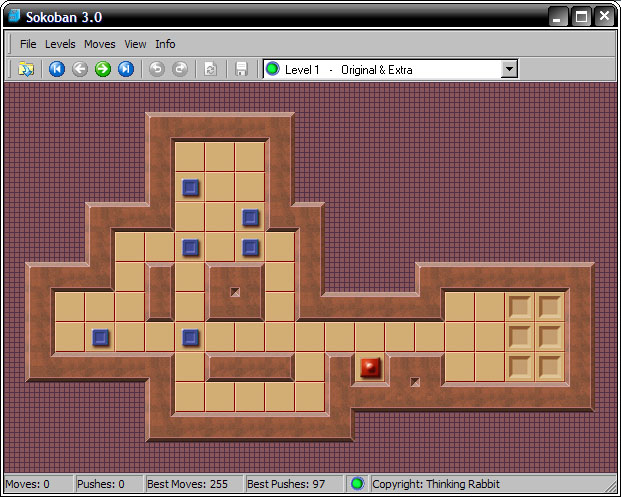
The solution screen for level one immediately before the last crate push is:
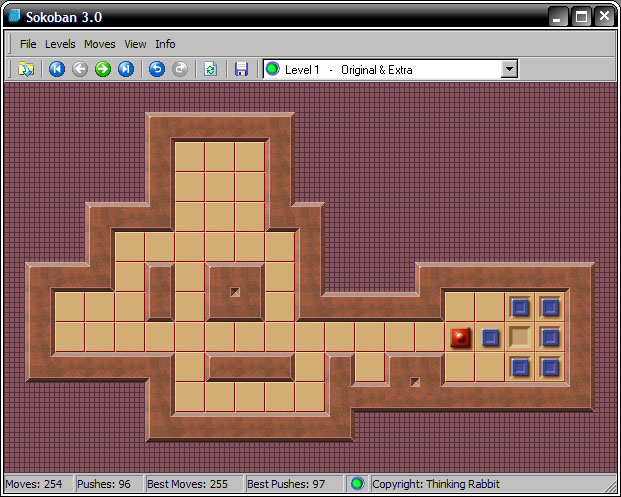
To record a solution to a level you must capture the screen immediately preceding the last crate push. When a level is solved the game immediately displays the following dialog:
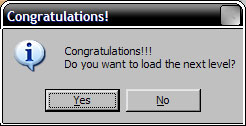
Selecting either option erases your solution. (If you cannot completely solve a problem capture a screen showing your partial solution for partial credit.) The status bar under the View menu must be selected to display the moves/pushes for the screen capture.
Your submission must contain no more than 3 window captures. Your submission file size must be kept to a minimum. Web-CAT will reject large files. To accomplish this, your screen capture must be of only the sokoban window, (not your desktop). (In Windows use the snipping tool.) Do not paste the captured image directly into your document. First save it as a low-quality (3-4) JPG image then insert it into your document from the saved jpg file. Before submitting your document to the Web-CAT save it under a different file name. (This will force MS Word to discard the document undo history list which can be large and then convert it to a PDF.)
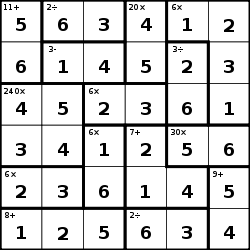
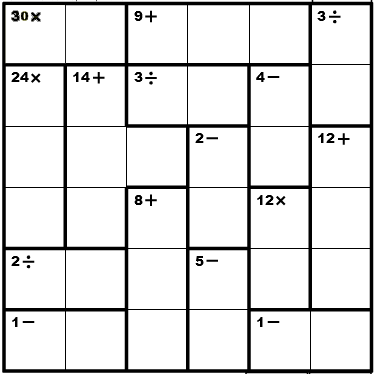
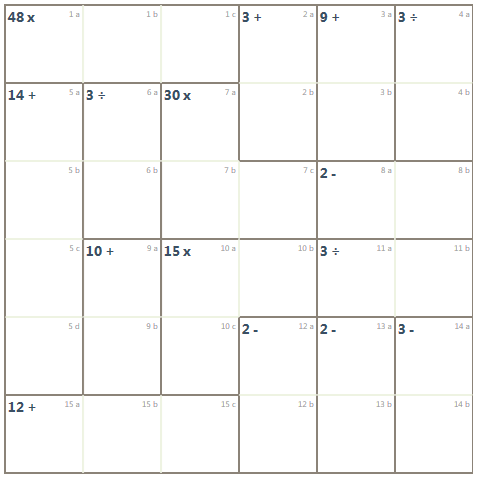
B. KenKen
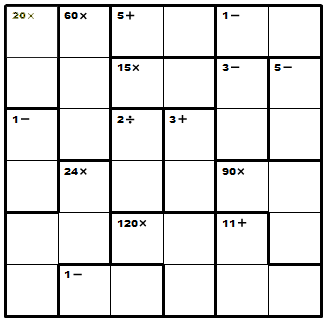
KenKen is a sudoku like game played on a square grid with NxN cells where the objective is to place a digit 1..N into each cell such that no row or column contains duplicate digits. The grids are separated into groups of cells, cages, which specifies a value and a mathematical operation. The value must be obtained by applying the operations to the values in the cage. The numbers within a cage may be repated as long as they do not occur in the same row or column. A single cell cage is a free space with no mathematical restriction and can be filled with any digit 1..9 adhering to the previous restrictions.
C. Sudoku
Sudoku and simlar games involve completing a grid of numbers while satisfying restrictions on the numbers and grid.

The variations of sudoku that we will use in this assignment are: Killer Sudoku, Futoshiki and Kakuro.
Group / Problem Assignments
Group/Problem 1: Sokoban problem #5 or #10
Group/Problem 2: KenKen #1
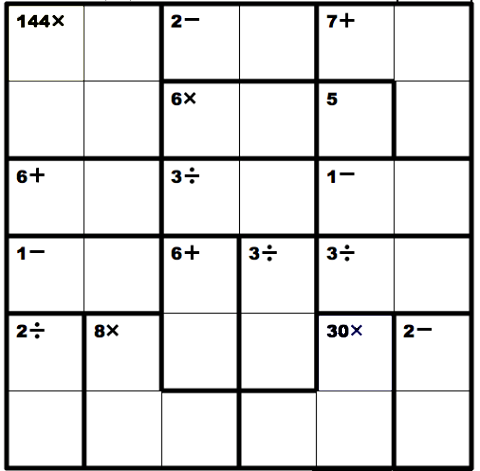
Group/Problem 3: Killer Sudoku
Fill the grid with numbers from 1 to 9 in a way that the following conditions are met:
- Each row, column, and 3x3 grid contains each number exactly once.
- The sum of all numbers in each grouping of cells denoted by a dotted line must match the small number printed in its corner.
- No number appears more than once in each grouping of cells denoted by a dotted line. (This is the standard rule for killer sudokus, and implies that no cage can include more than 9 cells.)
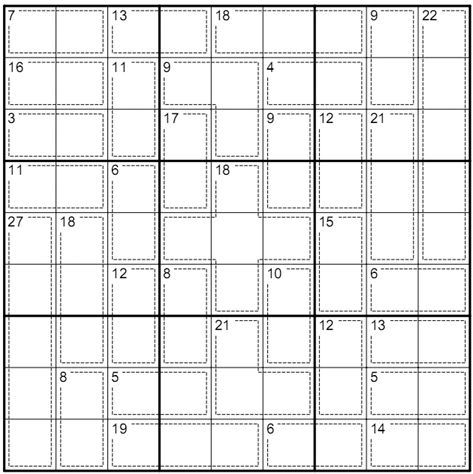
Group/Problem 4: Sokoban problem #6 or #11
Group/Problem 5: KenKen #2
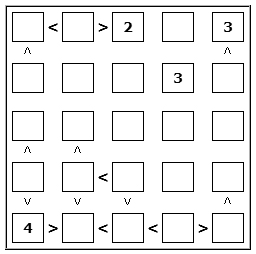
Group/Problem 6: Futoshiki
Each box is filled with a digit from 1 to 5, such that
every row and column contains one of each such
digit. The puzzle starts with a few boxes filled in for
you. There are also less than (<)
and greater than (>) constraints noted on some of the
boxes. Fill in the boxes in a
way that meets all of these requirements.
Group/Problem 7: Sokoban problem #7 or #12
Group/Problem 8: KenKen #3
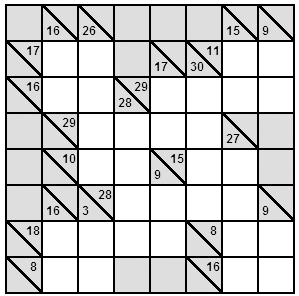
Group/Problem 9: Kakuro
Sometimes called “Cross Sums”, a kakuro grid is a little like a crossword grid and can be of any size. However in a kakuro grid, the numbers indicate the sum total of all the individual cells in that row or column. Each grid has a starting position like that of a crossword, containing grayed out squares and white squares. You need to fill in the blank (white) squares with a number from 1 to 9, but each run of numbers (an answer) can only contain each number once.
Group/Problem 10: Sokoban problem #8 or #13
Group/Problem 11: KenKen #4
Group/Problem 12: Sokoban problem #9 or #14
Think about the problems rather than just using trial & error.