CS 6104 : Solutions to Homework Assignment 5

June 19, 1998

Problem 1. [Solution Courtesy of Hussein Suleman]

Completely factor the polynomial

over using both the Berlekamp and Cantor-Zassenhaus algorithms. You may use Mathematicato do the calculations at each intermediate step, but show the results of all the steps.

Berlekamp Algorithm

First we define the given constants.

In[1]:= p=7
Out[1]= 7
In[2]:= f = x^8 +4 x^5 + 3x^2 + 5
Out[2]= 5 + 3*x^2 + 4*x^5 + x^8

polydegree is a function that calculates the degree of a polynomial by counting the number of coefficients of positive powers of x. This is then used to calculate the degree of f.

In[3]:= polydegree[y_]:=Length[CoefficientList[y, x]]-1
In[4]:= degf = polydegree[f]
Out[4]= 8

is defined and used to calculate the table of values for all powers of x in the basis of .

In[5]:= tau[x_] := x^p
In[6]:= taulist=Table[PolynomialMod[tau[x^i], f, {Modulus->p}], {i, 0, degf-1}]
Out[6]= {1, x^7, 5 + 3*x^2 + 6*x^3 + 2*x^5 + 2*x^6, 
  4*x + 3*x^2 + x^3 + 3*x^4 + 4*x^5, 
  5 + 2*x + 5*x^2 + 3*x^3 + 5*x^4 + 2*x^5 + 5*x^6 + 3*x^7, 
  x + x^2 + 2*x^3 + 6*x^4 + 3*x^5 + 5*x^6 + 2*x^7, 
  6 + 6*x + 4*x^2 + x^3 + 4*x^4 + 4*x^5 + 4*x^6 + x^7, 
  6 + 4*x + 3*x^2 + x^3 + 4*x^4 + 3*x^5 + 3*x^6 + 5*x^7}

The coefficients are extracted and arranged into the matrix T. T-I is calculated and row-reduced.

In[7]:= T=Transpose[
    Map[(Join[CoefficientList[#, x],Table[0,{degf-polydegree[#]-1}]])&, 
      taulist]]
Out[7]= {{1, 0, 5, 0, 5, 0, 6, 6}, {0, 0, 0, 4, 2, 1, 6, 4}, 
  {0, 0, 3, 3, 5, 1, 4, 3}, {0, 0, 6, 1, 3, 2, 1, 1}, 
  {0, 0, 0, 3, 5, 6, 4, 4}, {0, 0, 2, 4, 2, 3, 4, 3}, 
  {0, 0, 2, 0, 5, 5, 4, 3}, {0, 1, 0, 0, 3, 2, 1, 5}}
In[8]:= TminusI = Mod[T-IdentityMatrix[degf], p]
Out[8]= {{0, 0, 5, 0, 5, 0, 6, 6}, {0, 6, 0, 4, 2, 1, 6, 4}, 
  {0, 0, 2, 3, 5, 1, 4, 3}, {0, 0, 6, 0, 3, 2, 1, 1}, 
  {0, 0, 0, 3, 4, 6, 4, 4}, {0, 0, 2, 4, 2, 2, 4, 3}, 
  {0, 0, 2, 0, 5, 5, 3, 3}, {0, 1, 0, 0, 3, 2, 1, 4}}
In[9]:= RRTMinusI=RowReduce[TminusI, {Modulus->p}]
Out[9]= {{0, 1, 0, 0, 0, 0, 0, 6}, {0, 0, 1, 0, 0, 0, 0, 4}, 
  {0, 0, 0, 1, 0, 0, 0, 1}, {0, 0, 0, 0, 1, 0, 4, 0}, 
  {0, 0, 0, 0, 0, 1, 5, 6}, {0, 0, 0, 0, 0, 0, 0, 0}, 
  {0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0}}

We then calculate . The basis for this kernel has three vectors, so there must be three irreducible factors in f.

In[10]:= ns=NullSpace[RRTMinusI, Modulus->p]
Out[10]= {{0, 1, 3, 6, 0, 1, 0, 1}, {0, 0, 0, 0, 3, 2, 1, 0}, 
  {1, 0, 0, 0, 0, 0, 0, 0}}

Now we choose a random element in the kernel of T-I. ca is the element and a is its polynomial representation.

In[11]:= ca=ns[[2]]
Out[11]= {0, 0, 0, 0, 3, 2, 1, 0}
In[12]:= a=ca.Table[x^i, {i, 0, degf-1}]
Out[12]= 3*x^4 + 2*x^5 + x^6

Finally, we can generate a list of factors by taking the of f with each of , for all .

In[13]:= BerlFactors = 
  Select[Table[
      PolynomialGCD[PolynomialMod[a-i, p], f, Modulus->p], {i, 0, p-1}],(
        polydegree[#]>0 && polydegree[#]<degf)&]
Out[13]= {3 + 5*x + 4*x^3 + x^4, 3 + x, 6 + 2*x + x^3}

To verify the result, we can check that none of the factors are multiples of any other, and that the product of the three factors yields f. Then, since the basis has 3 vectors and we have found 3 irreducible factors, we know that we have found all the factors of f.

In[14]:= Map[(PolynomialGCD[BerlFactors[[#[[1]]]], BerlFactors[[#[[2]]]], 
        Modulus->p])&, {{1,2},{1,3},{2,3}}]
Out[14]= {1, 1, 1}
In[15]:= Expand[Apply[Times, BerlFactors], Modulus->p]
Out[15]= 5 + 3*x^2 + 4*x^5 + x^8

Cantor-Zassenhaus Algorithm

This algorithm is identical to the Berlekamp one up until the calculation of the nullspace. Thereafter, we test random elements from the nullspace for the given conditions.

a1 is the first random element used and it generates the factor g1.

In[16]:= ca1=Mod[ns[[1]]+2ns[[2]]+3ns[[3]], p]
Out[16]= {3, 1, 3, 6, 6, 5, 2, 1}
In[17]:= a1=ca1.Table[x^i, {i, 0, degf-1}]
Out[17]= 3 + x + 3*x^2 + 6*x^3 + 6*x^4 + 5*x^5 + 2*x^6 + x^7
In[18]:= g1=PolynomialGCD[a1, f, Modulus->p]
Out[18]= 1
In[19]:= s1 = PolynomialMod[Expand[a1^((p-1)/2)], f, Modulus->p]
Out[19]= 4 + 2*x + 6*x^2 + 5*x^3 + 2*x^5 + 2*x^7
In[20]:= g1 = PolynomialGCD[s1-1, f,Modulus->p]
Out[20]= 3 + 5*x + 4*x^3 + x^4

a2 is the second random element used and it generates the factor g2.

In[21]:= ca2=Mod[2ns[[2]]+ns[[3]], p]
Out[21]= {1, 0, 0, 0, 6, 4, 2, 0}
In[22]:= a2=ca2.Table[x^i, {i, 0, degf-1}]
Out[22]= 1 + 6*x^4 + 4*x^5 + 2*x^6
In[23]:= g2=PolynomialGCD[a2, f, Modulus->p]
Out[23]= 3 + x

a3 is the third random element used and it generates the factor g3.

In[24]:= ca3=Mod[2ns[[1]]+3ns[[2]], p]
Out[24]= {0, 2, 6, 5, 2, 1, 3, 2}
In[25]:= a3=ca3.Table[x^i, {i, 0, degf-1}]
Out[25]= 2*x + 6*x^2 + 5*x^3 + 2*x^4 + x^5 + 3*x^6 + 2*x^7
In[26]:= g3=PolynomialGCD[a3, f, Modulus->p]
Out[26]= 6 + 2*x + x^3

CZFactors is the list of factors. To verify the result, we can once again check that none of the factors are multiples of any other, and that the product of the three factors yields f. Then, since the basis has 3 vectors and we have found 3 irreducible factors, we know that we have found all the factors of f.

In[27]:= CZFactors={g1, g2, g3}
Out[27]= {3 + 5*x + 4*x^3 + x^4, 3 + x, 6 + 2*x + x^3}
In[28]:= Map[(PolynomialGCD[CZFactors[[#[[1]]]], CZFactors[[#[[2]]]], 
        Modulus->p])&, {{1,2},{1,3},{2,3}}]
Out[28]= {1, 1, 1}
In[29]:= Expand[Apply[Times, CZFactors], Modulus->p]
Out[29]= 5 + 3*x^2 + 4*x^5 + x^8

Thus, in summary, both algorithms yield the list of factors:

Problem 2. [Solution Courtesy of Scott Guyer]

Consider the following instance of the Merkle-Hellman public-key encryption scheme:

Do the following.

1. Implement the algorithm for solving low density SUBSET SUM problems in Mathematica. Note that the lattice basis reduction algorithm is built into Mathematicaas the function LatticeReduce.
2. Show how to use the algorithm to decrypt the message

   

3. Bonus subproblem: Recover the hidden keys c and d and the superincreasing sequence

   

   used to construct the above scheme. THIS SUBPROBLEM IS OPTIONAL!

1. Implement the algorithm for solving low density SUBSET SUM problems in Mathematica. Note that the lattice basis reduction algorithm is built into Mathematicaas the function LatticeReduce.

   The implementation is the same as that in the handout. We just want to make sure that the arithmetic is modular at certain points in the algorithm.

   

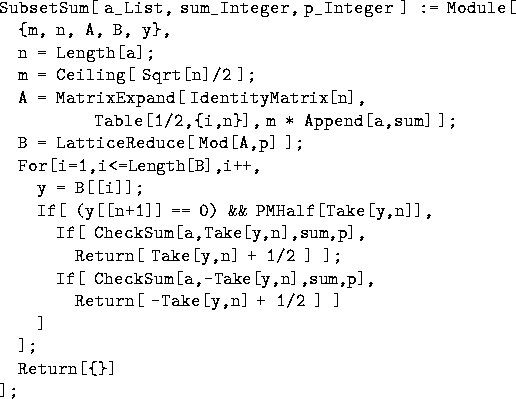
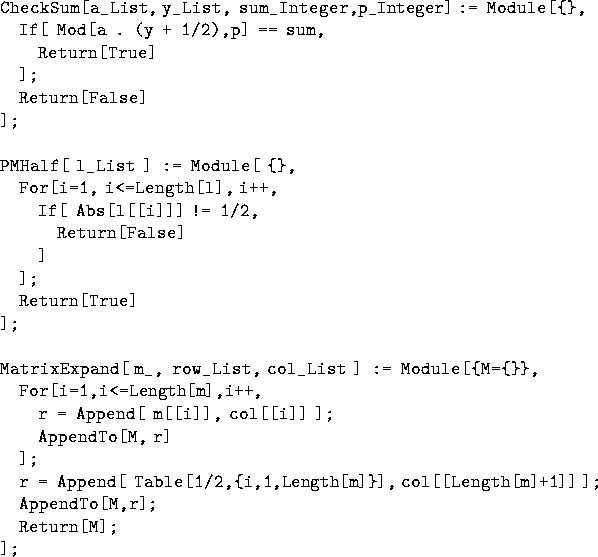
   Note that the algorithms uses 3 helper functions. In particular, MatrixExpand, PMHalf, and CheckSum. MatrixExpand takes the given matrix and augments it with the given row and column vectors. The assumptions are that if the given matrix is square with dimension n, then the row and column vectors have length n+1; and that the n+1 row and column entries are identical. PHHalf just checks to see that every entry in the given vector is plus or minus one-half. Finally, CheckSum uses vector dot products to compute the linear sum of its given vectors modulo the modulus p and compares it to sum. All three of these routines are shown below.

   

2. Show how to use the algorithm to decrypt the message

   

   Using the implementation of the SubsetSum function presented above, the message 1238514 can be decode by executing the following Mathematica code.

   In[2]:= SubsetSum[ {455933, 735485, 640682, 878709, 1102018, 869434},
     1238514,
     1239671 ]
   Out[2]= {0, 1, 1, 0, 1, 0}

3. Bonus subproblem: Recover the hidden keys c and d and the superincreasing sequence

   

   used to construct the above scheme.

   To break the code, all we need is a d such that the sequence is superincreasing. Once such value is d = 745. In this case, we get the superincreasing sequence

   

   Indeed, this is superincreasing, and

   

   To recover c, we can just solve because we know that p is prime. Hence, c = 688891.