CS 6104 : Solutions to Homework Assignment 4

July 9, 1998

Problem 1. [Solution Courtesy of Wen Wang]

Chapter 6, problem 9.

Suppose

if and only if:

1. s=2t; and
2. 

That is,

1)

s=2t; and

2)

.

If k is of characteristic 2, then the conditions are:

1. s=2t
2. For the coefficients:

   

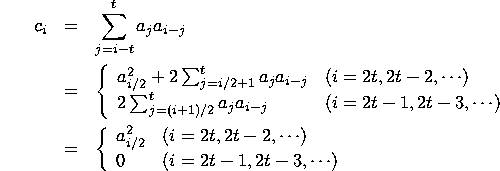
If k is not of characteristic 2, then the conditions are:

1)

s=2t; and

2)

For the coefficients:

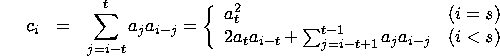
That is,

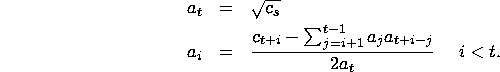
This requires that be a square.

Hence, if k is of characteristic 2, f is a square in k((1/x)) if and only if deg(f) is even, and . If k is not of characteristic 2, f is a square in k((1/x)) if and only if deg(f) is even, and the first coefficient is a square in k.

Problem 2. [Solution Courtesy of Craig Struble]

This problem is inspired by problem 13 in Chapter 6. For , define

where is the Euler phi function.

1. For what value of m, where , is maximized?
2. More generally, for what values of m (as m goes from 1 to ), does reach new maxima? (A new maximum is an m such that , whenever m';SPMlt;m.)
3. Use methods from Chapter 2 to show Landau's result that .
4. Fix a prime p. Give an asymptotic lower bound on the probability that a randomly selected polynomial in of degree n is primitive.

1. The value at which is maximized where is

   

   Part B explains why this is the maximum value.

2. Suppose is the unique prime factorization of m. Equation (2.2) on page 23 of the text states

   

   Simplifying ,

   

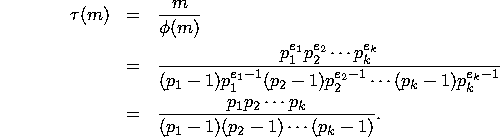
   The value of depends only on the prime factors of m, regardless of their exponents. So, consider only values of m that are the product of unique primes. Each prime p contributes a factor of

   

   to . Clearly, if x ;SPMlt; y, then . So is maximized by multiplying primes that are as small as possible; that is, is maximized when m is the product of the first k primes, and the maximum changes when m is multiplied by the next prime. So, to find the value m that maximizes when , multiply consecutive primes together until .

3. For this part, assume that is the product of the first k primes. We see from Part B that

   

   To use the techniques in Chapter 2, we need to manipulate the product and find a sum that can be bounded. Consider writing

   

   where e is the exponential and is a polynomial such that

   

   Hence,

   

   Using the laws of logarithms and Maclaurin expansion,

   

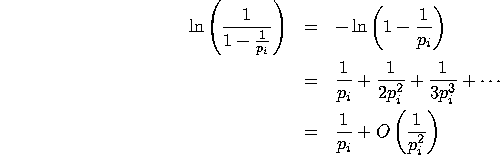
   So, . Now can be written as

   

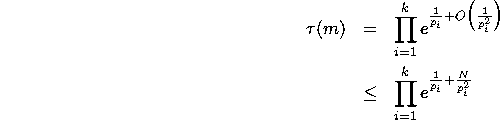
   where N is a constant as defined for the O notation. Exponents add when multiplying powers together, so now we can apply techniques from Chapter 2. Begin by bounding the sum of the terms.

   

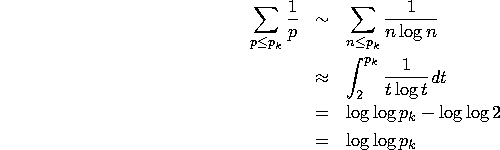
   To bound the sum , note that converges. Thus the sum also converges to a constant, call it D. Now, ignoring constant factors, we get

   

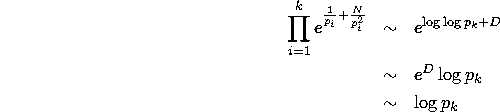
   One final step is necessary to reach our goal. How is related to m? Consider ,

   

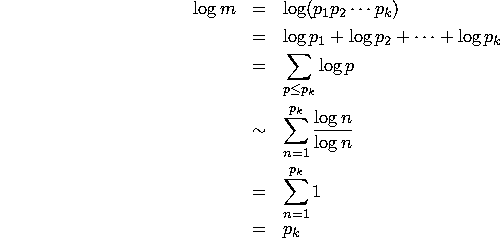
   Hence, .

4. The number of monic primitive polynomials of degree n in is

   

   The total number of monic polynomials of degree n in is . So the probability of selecting a primitive polynomial of degree n in is

   

   In Part C, we gave an upper bound for . Use this to obtain a lower bound for .

   

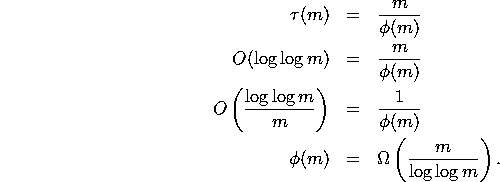
   The probability is then bounded by

   

Problem 3. [Solution Courtesy of Degong Song]

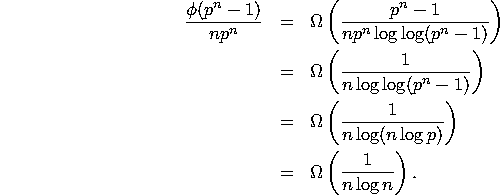
Chapter 7, problem 4. Flesh out the solution in the back of the book.

From (mod) 4 we get 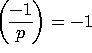. This means that the equation does not have solution in , so .

From and definition of , we know

where c and d can not be 0 simultaneously.

First we show that if and only if c=d=0. Otherwise, assume , then and hence from we see that while . This is in contradiction with .

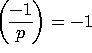Thus, from

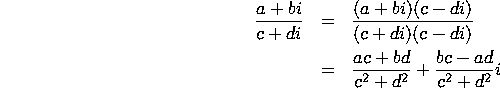
and , it is not difficult to verify that

(or ) has elements and it is an extension field of with operation compatible to that of . From book, any two finite fields with elements are isomorphic, and from above discussion, one Model of can be given as .

Since 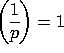and 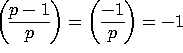, we can use binary search to find a x such that , 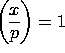and 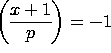. The algorithm for doing this is given bellow (in the algorithm, legendre[x,p] means ):

          procedure FindX(left,right)
          { 
                if(right-left=1)
                       return left;
                mid=Floor[(left+right)/2];
                if(legendre[mid,p]=1)
                       return FindX(mid,right);
                else
                       return FindX(left,mid);
          }

We use FindX(1,p-1) to call the program and get x.

Use power algorithm and 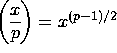(mod p), the time complexity to get is bit operation. Due to binary search, there will be such operations. After considering all the other operations, the complexity to find this x using above algorithm is .

Using the above x, we can construct a non-square element in . The fact that 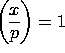and

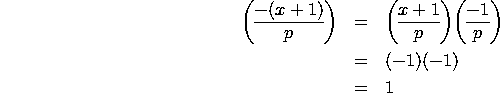
tell us that both x and -(x+1) have root in . Noting that p=3 mod 4, from Corollary 7.1.2, we have

and

and these u and v can be computed using bit operation.

Now, the element u+vi must be a non-square element in . Otherwise, there exists a+bi with such that

which implies , v=2ab, and hence

On the other hand, from , we see that . This together with above equation implies . Since , we get 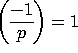. This is in contradiction with .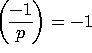

Any square roots in can be computed using Tonelli's algorithm. Tonelli's algorithm is nondeterministic only because it randomly chooses an element and hope it is not a square (and thus it will be a generator). Now that we have found a non-square element u+vi in using above procedure, we can use this u+vi as g in Tonelli's algorithm. In this situation, Tonelli's algorithm would become deterministic.

The time complexity for computing u+vi is bit operation. The running time for the modified Tonelli's algorithm is also bit operation (cf. Theorem 7.1.3). So, the total running time for computing square roots in using this method is bit operation. So, it is deterministic polynomial time.