HW #2: 10 problems

Due Wednesday 8 September 1999 at 1200 hrs

Late policy: 10%/day up to 50% (weekends = 1 day)

If your paper is illegible, you will lose points

1. Create a DFSA for a soda machine. Assume that $.20 will buy a soda (ha! otherwise, the machine gets quite large) and that legal inputs are {$.05, $.10, $.25, coke, classic_coke, sprite}. Other inputs ($.01) cause the machine to loop on its current state. Try to build a reasonably realistic machine.
2. (Hopcroft and Ullman) Consider the toy shown below. A marble is dropped in at A or B. Levers x₁, x₂, and x₃ cause the marble to fall either to the left or right. Whenever a marble encounters a lever, it causes the lever to change state, so that the next marble to encounter the lever will take the opposite branch.

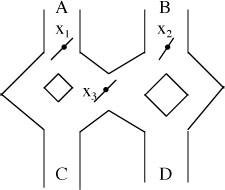
• model this toy by a finite automaton. Denote a marble in at A by a 0-input and a marble in at B by a 1-input. A sequence of inputs is accepted if the last marble comes out at D.
• describe the set accepted by the finite automaton.
3. (Gregory Taylor) Give the finite state machine to recognize an identifier in the C++ programming language. Don’t worry about reserved words! Your fsa will simply accept any reserved word as an identifier.
4. (Greenlaw and Hoover) Can a DFSA have an infinite computation? (You will have to think about what a computation is in such a machine.) Justify your answer.

Problem 2.1.3 of our text

Problem 2.1.4

Problem 2.1.5

Note: please read but do not turn in problem 2.1.6

Problem 2.2.4

Problem 2.2.6

Problem 2.2.9