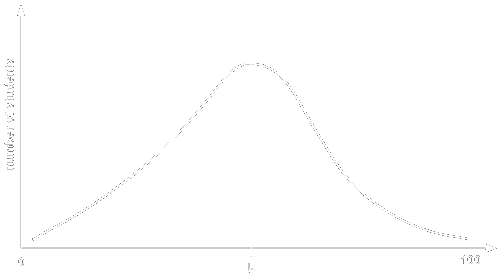
uncurved 'skewed' t-distribution


curved 'normal' t-distribution
| Computer Science 1704 |
Intro to Data Structures & Soft Eng
|
The Krider Curve was developed by Dr. Daniel W. Krider, Prof. of Mathematics, Concord College, Athens, WV. The curve coerces grades into forming a distribution which more closely resembles a Normal Distribution. This is a partial solution to the problem of class grades tending to be skewed toward the lower values. The Krider Curve forces symmetrical clustering about the mean (property of central tendency) and smaller variance within the scores (less dispersion).

uncurved 'skewed' t-distribution


curved 'normal' t-distribution
Given the following variables:
x Û student's grade
y Û student's curved grade
a Û curve percentage
The Krider curve formula, , is applied to each individual student grade.
For example, if a = 1/3 then
y = x + 1/3 ( 100 - x )
This is equivalent to averaging two x values with one grade of a 100. The lower scores receive a larger curve than the upper scores. An appropriate action when one considers that poorer students require more help. The curve ensures that a student will never surpass another student who scores higher.
Alpha can be set to achieve a desired class mean.
Given the following:
_
x Û class mean
m Û desired mean
n Û class size
The formula for deriving alpha's value for a desired mean:
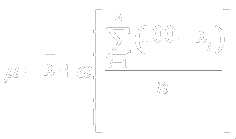
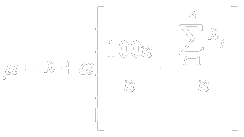
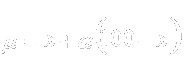
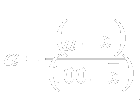
| D. Barnette 1/21/2000 | Virginia Tech © 1995-2000 |